Tensorflow学习笔记-CNN卷积神经网络架构

发表于 | 分类于

前言

卷积神经网络是近些年逐步兴起的一种人工神经网络结构, 因为利用卷积神经网络在图像和语音识别方面能够给出更优预测结果, 这一种技术也被广泛的传播可应用. 卷积神经网络最常被应用的方面是计算机的图像识别, 不过因为不断地创新, 它也被应用在视频分析, 自然语言处理 等等. 近期火热的 Alpha Go, 让计算机看懂围棋, 同样也是有运用到这门技术.

img

CNN卷积神经网络

比起传统神经网络，CNN到底有什么不同？我们回想一下：传统神经网络的每个神经元完全连接到前一层的所有神经元，而单层神经元完全独立运行，不共享任何连接。这会导致什么呢？举个例子：当处理一个32×32×3（32宽，32高，3色通道）的图像数据时，第一个隐藏层中的一个完全连接的神经元将具有32×32×3 = 3072的权重。虽然这个数据量看起来似乎还可以，但我们已经发现问题了：随着输入数据和层的增加，参数会快速飞涨起来！并且，这种完整的连接是浪费的，大量的参数很快就会导致过度配置。

就好像我们将整个世界的书籍都堆在了孩子的面前，并指望他不走弯路且高效地学习完这些，这是粗鲁的。

img

针对像图像这种的具有局部特征的数据，卷积神经网络充分利用了输入由图像组成的事实，并以更合理的方式建立了体系结构：与常规的神经网络不同，ConvNet的层具有三维排列的神经元：宽度，高度，深度。（请注意，“深度”这里指的是激活数据的第三维，而不是整个神经网络的深度。）一层中的神经元只能连接到它之前层的一个小区域，而不是以完全连接的方式连接到所有的神经元。

img

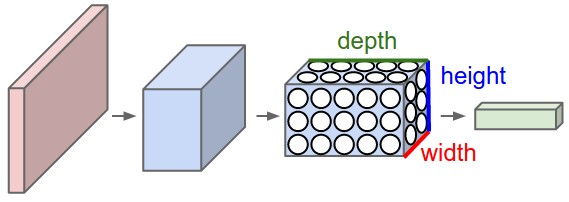
上图：一个ConvNet在三个维度（宽度，高度，深度）上安排它的神经元，如在一个图层中可视化的那样。ConvNet的每一层都将3D输入数据转换为神经元激活的3D输出数据。在这个例子中，红色输入层保存图像，所以它的宽度和高度将是图像的尺寸，并且深度将是3（红色，绿色，蓝色通道）。

CNN神经网络架构

img

在这里例举一个经典架构：

[ INPUT –> CONV –> RELU –> POOL –> FC ]

更详细地说：

  • INPUT [32x32x3]将保存图像的原始像素值，在这种情况下，图像的宽度为32，高度为32，并具有三个颜色通道R，G，B。
  • CONV层（卷积层）将计算连接到输入中的局部区域的神经元的输出，每个计算它们的权重与它们在输入体积中连接的小区域之间的点积。如果我们决定使用12个过滤器，这会导致输出为[32x32x12]。
  • RELU层将应用元素激活函数，如max（0，x），但不改变数据尺寸。
  • POOL层（池化层）将沿着空间维度（宽度，高度）执行下采样操作，从而产生诸如[16x16x12]的音量。
  • FC层（完全连接层）将计算类别分数，得到大小为[1×1×10]的数量，其中每个数字对应于一个类别分数，例如在CIFAR-10的10个类别中。和传统的神经网络一样，这个层中的每个神经元都将被连接到前一层中的所有神经元。

img

一个示例ConvNet神经网络。初始卷存储原始图像像素（左），最后一卷存储类别分数（右）。处理路径上的每个激活量显示为一列。由于很难将3D卷积可视化，因此我们将每个卷的切片放在一行中。最后一个图层卷保存每个类的分数，但是在这里我们只显示排序的前五个分数，并打印每个分数的标签。完整的演示在这里：web-based demo 。

现在介绍各个层和需定义的超参数及其连接的细节。

Convolutional Layer（卷积层）

Conv层是卷积网络的核心组成部分，完成大部分计算繁重工作。

img

CONV层的参数由一组可学习的过滤器组成。每个过滤器在空间上都很小（沿着宽度和高度），但是贯穿输入体积的整个深度。例如，ConvNet的第一层上的典型过滤器可能具有5x5x3的大小（即，5像素的宽度和高度，3颜色通道）。过滤器沿着输入体积的宽度和高度滑动（更精确地说是卷积）每个过滤器，计算过滤器视野中的数据和Weight之间的点积。当我们在输入体积的宽度和高度上滑动滤波器时，我们将生成一个二维激活图，给出每个空间位置滤波器的响应。沿深度维度堆叠这些激活图并产生输出量。

img

一个示例：输入体积（例如，32x32x3 CIFAR-10图像）以及第一卷积层中的示例体积的神经元。卷积层中的每个神经元仅在空间上连接到输入体积中的局部区域，但是连接到全深度（即所有颜色通道）。请注意，沿着深度有多个神经元（在这个例子中是5个），所有神经元都在输入中查看相同的区域。

介绍下需要定义的超参数：

  • 过滤器 视野（F）是个超参数，过滤器将每个神经元连接到输入数据的局部区域。
  • 输出量的 深度（k）是一个超参数：它对应于我们想要使用的过滤器的数量，每个过滤器学习在输入中寻找不同的东西。
  • 其次，我们必须指明我们滑动过滤器的 步伐（S）。当步幅为1时，我们一次将滤镜移动一个像素。当步幅是2（或者不常见的是3或更多，尽管这在实践中很少见），那么当我们滑动它们时，滤波器一次跳跃2个像素。这将在空间上产生较小的输出量。
  • 正如我们将很快看到的，有时将输入音量填充到边界周围将会很方便。这个 填充（P）的大小是一个超参数。零填充的好处在于，它允许我们控制输出体积的空间大小（最常见的是我们很快就会看到，我们将使用它来精确地保留输入体积的空间大小，以便输入和输出宽度和身高是一样的）

我们可以通过以上超参数来计算输出数据尺寸：(W−F+2P)/S+1

img

空间排布的例证。在这个例子中，只有一个空间维度（x轴），一个神经元与F = 3的感受域的大小，输入尺寸为W = 5，并且存在零填充P = 1的左：神经元跨距（5 - 3 + 2）/ 1 + 1 = 5 右：神经元使用S = 2的步长，给出大小为（5 - 3 + 2） / 2 + 1 = 3。请注意，步幅S = 3无法使用，因为它不能很好地穿过数据。（5-3 + 2）= 4不能被3整除。
在这个例子中神经元的权重是[1,0，-1]（在右边显示），它的偏差是零。这些权重在所有黄色神经元上共享。

卷积演示

以下是一个CONV层的演示。由于三维体积难以可视化，所有的体积（输入体积（蓝色），体重体积（红色），输出体积（绿色））可视化，每个深度切片堆叠成行。输入体积为W1=5,H1=5,D1=3，CONV层参数为K=2,F=3,S=2,P=1。也就是说，我们有两个尺寸为3×3的滤镜，并且它们以2的步幅施加。因此，输出体积大小具有空间大小（5-3 + 2）/ 2 + 1 = 3。此外，填充P=1被施加到输入体积，使输入音量的外边界为零。下面的可视化对输出激活（绿色）进行迭代，并显示每个元素的计算方法是将高亮显示的输入（蓝色）与过滤器（红色）进行元素相乘，然后将其相加，然后通过偏移来输出结果。

img

摘要

总而言之，Conv层：

  • 输入大小为：W1×H1×D1
  • 需要四个超参数：
    • 过滤器数 ķ
    • 过滤器大小 F
    • 步幅 S
    • 填充量 P
  • 输出大小为：W2×H2×D2
    • W2=(W1−F+2P)/S+1
    • H2=(H1−F+2P)/S+1
    • D2=K

注：当P=0且S=1时，W和H不变，D2=K 。

超参数的常见设置是F= 3 ，S= 1 ，P= 1

Pooling Layer（池化层）

每次卷积都会丢失数据，于是有了池化，即每次卷积，不减小尺寸，压缩交给池化。

周期性地在ConvNet体系结构中连续的Conv层之间插入一个Pooling层。其功能是逐步减小表示的空间大小，以减少网络中的参数和计算量，从而也控制过拟合。池层在输入的每个深度切片上独立运行，并使用MAX操作在空间上调整其大小。

最常见的形式是一个大小为2x2的过滤器的汇聚层，在输入的每个深度切片上沿着宽度和高度两次施加2个下采样的步幅，丢弃75％的激活。在这种情况下，每个MAX操作最多需要4个以上的数字（在某个深度切片中只有很少的2×2区域）。深度维度保持不变。

摘要

总而言之，池化层：

  • 输入大小为：W1×H1×D1
  • 需要四个超参数：
    • 过滤器大小 F
    • 步幅 S
  • 输出大小为：W2×H2×D2
    • W2=(W1−F)/S+1
    • H2=(H1−F)/S+1
    • D2=D1

常见设置是F= 3 ，S= 2（重叠池） 或者F= 2 ，S= 2 （这个更常见）。

img

池化层在输入体积的每个深度切片中独立地在空间上下采样该体积。左图：在此示例中，尺寸为[224x224x64]的输入量与过滤器尺寸2合并，跨度为2尺寸为[112x112x64]的输出量。请注意，数据深度保留。右：最常见的下采样操作是最大的，产生MAX POOLING，这里显示的步幅是2,也就是说，每个最大值是4个数字（小2×2平方）。

Fully-connected layer（全连接层）

完整连接层和传统神经网络的架构一样。完整连接层中的神经元与前一层中的所有激活完全连接，正如在常规神经网络中所看到的那样。因此可以用一个矩阵乘法和一个偏置偏移来计算它们的激活。

案例演示

好了，现在对卷积神经网络内部数据流动，已经有了大概的了解，现在我们通过代码来实现一个基于MNIST数据集的简单卷积神经网络。

定义卷积层的 weight&bias

首先我们导入

1
import tensorflow as tf

采用的数据集依然是tensorflow里面的mnist数据集

我们需要先导入它

1
python from tensorflow.examples.tutorials.mnist import input_data

本次用到的数据集就是来自于它

1
mnist=input_data.read_data_sets('MNIST_data',one_hot=true)

接着呢，我们定义Weight变量，输入shape，返回变量的参数。其中我们使用tf.truncted_normal产生随机变量来进行初始化.（标准差为0.1）

这里说明下tf.truncted_normal与tf.random_normal ，虽然都是从正态分布的曲线中输出随机值，但前者产生的随机数与均值的差距不会超过两倍的标准差.即从截断的正态分布中输出随机值。

1
2
3
def weight_variable(shape): 
	inital=tf.truncted_normal(shape,stddev=0.1)
	return tf.Variable(initial)

同样的定义biase变量，输入shape ,返回变量的一些参数。其中我们使用tf.constant常量函数来进行初始化:

1
2
3
def bias_variable(shape): 
	initial=tf.constant(0.1,shape=shape) 
	return tf.Variable(initial)

定义卷积，tf.nn.conv2d函数是tensoflow里面的二维的卷积函数，x是图片的所有参数，W是此卷积层的权重，然后定义步长strides=[1,1,1,1]值，strides[0]和strides[3]的两个1是默认值，中间两个1代表padding时在x方向运动一步，y方向运动一步，填充 padding采用的方式是SAME。

1
2
def conv2d(x,W):
	return tf.nn.conv2d(x,W,strides=[1,1,1,1]，padding='SAME')

定义 pooling

接着定义池化pooling，为了得到更多的图片信息，padding时我们选的是一次一步，也就是strides[1]=strides[2]=1，这样得到的图片尺寸没有变化，而我们希望压缩一下图片也就是参数能少一些从而减小系统的复杂度，因此我们采用pooling来稀疏化参数，也就是卷积神经网络中所谓的下采样层。

pooling有两种，一种是最大值池化，一种是平均值池化，本例采用的是最大值池化tf.max_pool()。池化的核函数大小为2x2，因此过滤器大小为2:ksize=[1,2,2,1]，步长为2，因此strides=[1,2,2,1]

  • tf.nn.max_pool
    • value：Tensor指定的格式的4-D data_format。
    • ksize：输入张量的每个维度的窗口的大小。
    • strides：输入张量的每个维度的滑动窗口的步幅。
    • padding：填充，'VALID'或者'SAME'。
    • data_format：一个字符串。支持“NHWC”，“NCHW”和“NCHW_VECT_C”。
    • name：操作的可选名称。
1
2
def max_pool_2x2(x): 
	return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],,padding='SAME')

定义 placeholder

首先呢，我们定义一下输入的placeholder

1
2
xs=tf.placeholder(tf.float32,[None,784])
ys=tf.placeholder(tf.float32,[None,10])

我们还定义了dropout的placeholder，它是解决过拟合的有效手段

1
keep_prob=tf.placeholder(tf.float32)

接着呢，我们需要处理我们的xs，改变形状，不要维度，形状28*28，黑白，把xs的形状变成[-1,28,28,1]，-1代表先不考虑输入的图片例子多少这个维度，后面的1是channel的数量，因为我们输入的图片是黑白的，因此channel是1，例如如果是RGB图像，那么channel就是3。

1
x_image=tf.reshape(xs,[-1,28,28,1])

建立卷积层

接着我们定义第一层卷积,先定义本层的Weight,本层我们的卷积核patch的大小是5x5，因为黑白图片channel是1所以输入是1，输出是32个featuremap

1
W_conv1=weight_variable([5,5,1,32])

接着定义bias，它的大小是32个长度，因此我们传入它的shape为[32]

1
b_conv1=bias_variable([32])

定义好了Weight和bias，我们就可以定义卷积神经网络的第一个卷积层h_conv1=conv2d(x_image,W_conv1)+b_conv1,同时我们对h_conv1进行非线性处理，也就是激活函数来处理喽，这里我们用的是tf.nn.relu（修正线性单元）来处理，要注意的是，因为采用了SAME的padding方式，输出图片的大小没有变化依然是28x28，只是厚度变厚了，因此现在的输出大小就变成了28x28x32

1
h_conv1=tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1)

最后我们再进行pooling的处理就ok啦，经过pooling的处理，输出大小就变为了14x14x32

1
h_pool=max_pool_2x2(h_conv1)

接着呢，同样的形式我们定义第二层卷积，本层我们的输入就是上一层的输出，本层我们的卷积核patch的大小是5x5，有32个featuremap所以输入就是32，输出呢我们定为64

1
2
W_conv2=weight_variable([5,5,32,64])
b_conv2=bias_variable([64])

接着我们就可以定义卷积神经网络的第二个卷积层，这时的输出的大小就是14x14x64

1
h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2)

最后也是一个pooling处理，输出大小为7x7x64

1
h_pool2=max_pool_2x2(h_conv2)

建立全连接层

好的，接下来我们定义我们的 fully connected layer,

进入全连接层时, 我们通过tf.reshape()将h_pool2的输出值从一个三维的变为一维的数据, -1表示先不考虑输入图片例子维度, 将上一个输出结果展平.

1
2
#[n_samples,7,7,64]->>[n_samples,7*7*64]
h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64])

此时weight_variable的shape输入就是第二个卷积层展平了的输出大小: 7x7x64， 后面的输出size我们继续扩大，定为1024

1
2
W_fc1=weight_variable([7*7*64,1024]) 
b_fc1=bias_variable([1024])

然后将展平后的h_pool2_flat与本层的W_fc1相乘（注意这个时候不是卷积了）

1
h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)

如果我们考虑过拟合问题，可以加一个dropout的处理

1
h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob)

接下来我们就可以进行最后一层的构建了，好激动啊, 输入是1024，最后的输出是10个 (因为mnist数据集就是[0-9]十个类)，prediction就是我们最后的预测值

1
W_fc2=weight_variable([1024,10]) b_fc2=bias_variable([10])

然后呢我们用softmax分类器（多分类，输出是各个类的概率）,对我们的输出进行分类

1
prediction=tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2)

选优化方法

接着呢我们利用交叉熵损失函数来定义我们的cost function

1
2
3
cross_entropy=tf.reduce_mean(
    -tf.reduce_sum(ys*tf.log(prediction),
    reduction_indices=[1]))

我们用tf.train.AdamOptimizer()作为我们的优化器进行优化，使我们的cross_entropy最小

1
train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

定义准确度计算函数

1
2
3
4
5
6
7
8
9
10
11
12
def compute_accuracy(v_xs,v_ys):
    global prediction
    # 预测值
    y_pre = sess.run(prediction,feed_dict={xs:v_xs,keep_prob:1})
    # 检查预测与是否符合事实，输出一个布尔的列表
    correct_prediction = tf.equal(tf.argmax(y_pre,1),tf.argmax(v_ys,1))
    # 取平均值变成准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
    # 传参并run一下
    result = sess.run(accuracy,feed_dict={xs:v_xs,ys:v_ys,keep_prob:1})
    tf.summary.scalar('compute_accuracy',result)
    return result

初始化指针

初始化变量

1
init = tf.global_variables_initializer()

接着呢就是和之前一样 定义Session

1
2
sess=tf.Session()
sess.run(init)

循环训练

接着就是训练数据了，我们假定训练1000步，每50步输出一下准确率， 注意sess.run()时记得要用feed_dict给我们的众多 placeholder 传数据.

1
2
3
4
5
for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step,feed_dict={xs:batch_xs,ys:batch_ys,keep_prob:1})
    if i % 50 == 0:
        print(compute_accuracy(mnist.test.images,mnist.test.labels))
用钱砸我，不要停！